本文最后更新于 about 1 year ago，文中所描述的信息可能已发生改变。

实正交群 $O(3)$. ​

实正交变换矩阵 ​

对于 $R^{3}$ 空间中的矢量，实正交变换前后，矢量的模长保持不变。也就是 $(gx)^{T}(gx) = x^{T}x$，其中 $g$ 为实正交变换矩阵，$x$ 为矢量。所以

$$g^{T}g = E \leftrightarrow g ^{-1} = g$$

两边同时取行列式可得

$$\det (g^{T})\det(g) = (\det(g))^{2} = 1$$

因此

$$\det(g) =\pm 1$$

所以实正交变换矩阵主要有两个特点，一个是其与其自身的转置的乘积为单位矩阵，另一个是行列式为 $\pm 1$。

实正交矩阵群 $O (3)$. ​

$$O (3)=\{g\mid g \text{为}3\times 3\text{矩阵},\:g^Tg=E\}$$

实特殊（幺模）正交群 $SO (3)$. ​

$$SO (3)=\{g\mid g \in O (3), \text{且} \det (g) = 1\}$$

$SO (3)$ 群中的任意矩阵都可以通过参数的连续变化变换到恒元。

$SO (3)$ 群的群空间是 双连通的。

$SO (3)$ 是 $O (3)$ 群的不变子群。

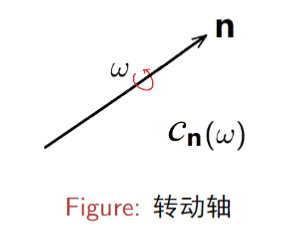
$SO (3)$ 群的共轭类 ​

对于 $\forall f= C_{\mathbf{k}}(\omega)\in SO (3)$，与 $f$ 共轭的元素为

$$GC_{\mathbf{k}}(\omega) g ^{-1}$$

因为

$$(gC_{\mathbf{k}}(\omega) g ^{-1})(g\mathbf{k}) = gC_{\mathbf{k}}(\omega )\mathbf{k} =g\mathbf{k}$$

所以共轭元素 $gC_{\mathbf{k}}(\omega) g ^{-1}$ 的转动轴为 $g \mathbf{k}$。

因此可以把共轭元素记为

$$GC_{\mathbf{k}}(\omega) g ^{-1} = C_{g\mathbf{k}}(\omega')$$

可以证明 $\omega = \omega'$，因此，$SO (3)$ 群中转动角度相同的群元在同一类中。

$C_{\hat{n}(\theta,\varphi)}(\omega)$ 的指数表示 ​

用 Pauli 矩阵和单位矩阵 $E$，作为由 $2\times 2$ 的厄米矩阵构成的复 Hilbert 空间的四个基矢。

$$E = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, \quad \sigma_{1} = \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}, \quad \sigma_{2} = \begin{bmatrix} 0 & -i \\ I & 0 \end{bmatrix}, \quad \sigma_{3} = \begin{bmatrix} 1 & 0 \\ 0 & -1 \end{bmatrix}$$

例如，将 $e^{-i \omega \sigma_{2}}$ 按照级数展开，则有：

$$\begin{aligned} E^{-i\omega\sigma_2}& =\quad\sum_{n=0}^{\infty}\frac 1{n!}(-i\omega\sigma_{2})^{n}\quad (\sigma_{2}^{0}=E,\:\sigma_{2}^{2}=E,\:\sigma_{2}^{3}=\sigma_{2},\:\sigma_{2}^{4}=E) \\ &=\quad E\left (1-\frac{\omega^2}{2!}+\frac{\omega^4}{4!}-\cdots\right)-i\sigma_2\left (\omega-\frac{\omega^3}{3!}+\frac{\omega^5}{5!}-\cdots\right) \\ &=\quad E\cos\omega-i\sigma_2\sin\omega \\ &\left.=\quad\cos\omega\left[\begin{array}{cc}1&0\\0&1\end{array}\right.\right]-i\sin\omega\left[\begin{array}{cc}0&-i\\i&0\end{array}\right] \\ &\left.=\quad\left[\begin{array}{cc}\cos\omega&-\sin\omega\\\sin\omega&\cos\omega\end{array}\right.\right] \end{aligned}$$

转换到 3 维，比如：

$$\sigma_{2}\to T_{3} = \begin{bmatrix} 0 & -i & \\ I & 0 & \\ & & 0 \end{bmatrix}$$

将 $e^{-i\omega T_{3}}$ 按照级数展开，可得：

$$T_{3} = \begin{bmatrix} 0 & -i & \\ I & 0 & \\ & & 0 \end{bmatrix}, \quad e^{-i\omega T_{3}} = \begin{bmatrix} \cos \omega & -\sin \omega & 0 \\ \sin \omega & \cos \omega & 0 \\ 0 & 0 & 1 \end{bmatrix} = C_{\mathbf{k}}(\omega)$$

同理可得

$$T_{2} = \begin{bmatrix} 0 & & i \\ & 0 & \\ -i & & 0 \end{bmatrix}, \quad e^{-i\omega T_{2}} = \begin{bmatrix} \cos \omega & 0 & \sin \omega \\ 0 & 1 & 0 \\ -\sin \omega & 0 & \cos \omega \end{bmatrix} = C_{\mathbf{j}}(\omega)$$

$$T_{1} = \begin{bmatrix} 0 & & \\ & 0 & -i \\ & i & 0 \end{bmatrix}, \quad e^{-i\omega T_{1}} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & \cos \omega & -\sin \omega \\ 0 & \sin \omega & \cos \omega \end{bmatrix} = C_{\mathbf{i}}(\omega)$$

绕任意转动轴的转动 $C_{\hat{n}(\theta,\varphi)}(\omega)$，可以通过对绕 $z$ 轴的转动的相似变换得到：

$$\begin{aligned} C_{\hat{n}(\theta,\varphi)}(\omega)& =\quad S (\varphi,\theta) C_{\mathbf{k}}(\omega) S (\varphi,\theta)^{-1} \\ &=Se^{-i\omega T_3}S^{-1} \\ &=S\left (\sum_n^\infty\frac{(-i\omega T_3)^n}{n!}\right) S^{-1} \\ &= \sum_n^\infty\frac 1{n!}S (-i\omega T_3) S^{-1}S (-i\omega T_3) S^{-1}S\cdots S (-i\omega T_3) S^{-1} \\ &=\sum_n^\infty\frac 1{n!}(S (-i\omega T_3) S^{-1})^n \\ &= e^{-i\omega ST_3 S^{-1}}\quad (ST_3 S^{-1}=n_iT_i) \\ &=-e^{-i\omega n_iT_i} \end{aligned}$$

其中：

$$\left.\left[\begin{array}{c}\omega_1\\\omega_2\\\omega_3\end{array}\right.\right]=\left[\begin{array}{c}\omega n_1\\\omega n_2\\\omega n_3\end{array}\right]=\left[\begin{array}{c}\omega\sin\theta\cos\varphi\\\omega\sin\theta\sin\varphi\\\omega\cos\theta\end{array}\right]$$

点群 ​

晶体点群 ​